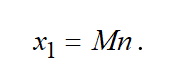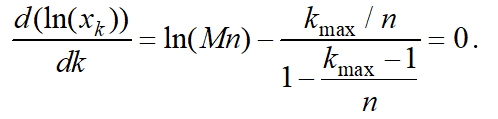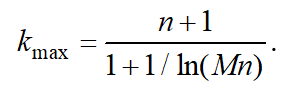Dynamic Scheduling for Flexible Manufactures - Design of the scheduling solutions tree

Design of the scheduling solutions tree

The solution tree is the outlined presentation for a scheduling decision issue. The branches of the tree are various events (solutions), and the nodes are key states where a decision is needed.    Usually, the tree of solution is designed top-to-bottom, starting from the root. Figure 4 depicts the tree scheduling layout. Here the apices (nodes) are designated by circles and the branches are half-lines, which come from nodes of some level to nodes of next level. Nodes of the last level are named as leaves.   

Figure 4. Tree of scheduling solutions.

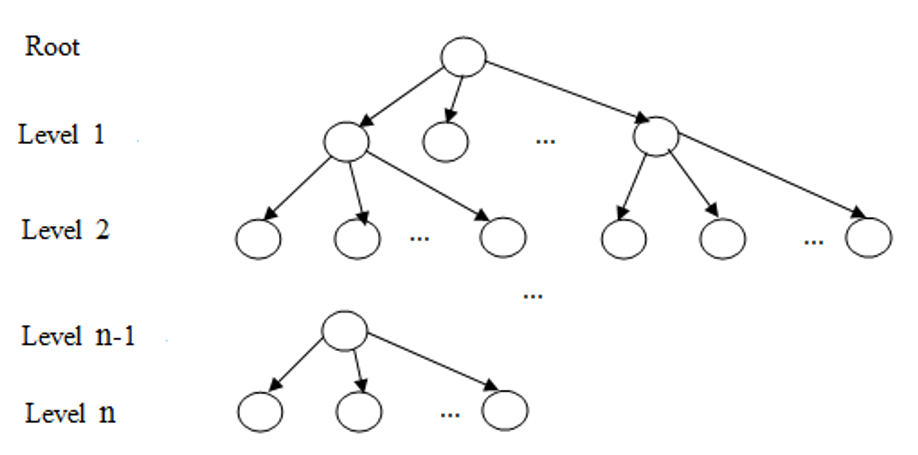
Any branch of the solution tree represents the event with a single job (or operation), which is carried out on a certain machine. In the node, all needed parameters are recorded: used fixtures; time of processing fulfillment; possible job volume and so on.

Let is assume the number of jobs, which is planned for horizon h, is equal to n, and each job may be realized on each machine of a set M. Then the number of half-lines from the root (level 1) is

(11)

Generally, on the next level, the number of planned jobs decreases by one:

(12)

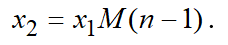
Following this process, we have on level 

(13) 

Mathematical relation (13) is geometrical progression with alternating denominator. There is distinction from usual geometric progression with constant denominator — the multiplier, which depends on a number of member in geometrical progression. Using formulas (11-13), for member in geometrical progression,

(14)

According to (14), the quantity of nodes with increasing level  number in the beginning grows quickly, but owing to the multiplier of product type, after some moment  the quantity diminishes. Let us find the level with maximum of node quantity. Logarithm for (14) is:

(15)

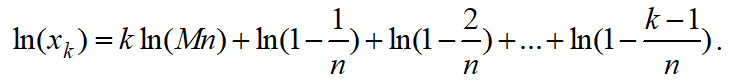
As logarithm for any variable is monotonous (increasing) function of this variable, maximum of the variable is in the point of maximum of its logarithm. Let us make the derivative of (15) and get it equal to zero.

 (16)

From (16), we have the level number with the most quantity of tree nodes:

(17)  

For example, if =15 and =4 the quantity maximum take place on the level number 13. According to formula (14) this maximum is equal to 10¹⁹.